
We propose a

$4\times$ undersampling patterns used for a variety of different diagnostic purposes.
CVPR 2025, Conference on Computer Vision & Pattern Recognition
We propose a unified MRI reconstruction model robust to various measurement undersampling patterns and image resolutions. Our approach uses neural operators, a discretization-agnostic architecture applied in both image and measurement spaces, to capture local and global features. Empirically, our model improves SSIM by 11% and PSNR by 4 dB over a state-of-the-art CNN (End-to-End VarNet), with 600× faster inference than diffusion methods. The resolution-agnostic design also enables zero-shot super-resolution and extended field-of-view reconstruction, offering a versatile and efficient solution for clinical MR imaging. Our unified model offers a versatile solution for MRI, adapting seamlessly to various measurement undersampling and imaging resolutions, making it highly effective for flexible and reliable clinical imaging.
Magnetic Resonance Imaging (MRI) is a widely-used non-invasive imaging technology, essential in medical and scientific fields such as neurosurgery, clinical oncology, diagnostic testing, neuroscience, and pharmaceutical research. However, its slow data acquisition process often requires patients to remain still for extended periods, limiting its efficiency and practicality.
Compressed Sensing (CS) techniques offer a solution by enabling MRI at sub-Nyquist rates, significantly reducing scan times. Traditional CS approaches rely on sparse priors in transform domains, while recent deep learning models take this a step further, learning deeper priors to improve reconstruction performance. Despite these advances, existing models often struggle to generalize across varying resolutions. Existing approaches need to be retrained for different undersampling patterns and rates, quickly becoming intractable.

We propose a

$4\times$ undersampling patterns used for a variety of different diagnostic purposes.
Neural Operators (NOs) are a cutting-edge deep learning framework that address this challenge by learning mappings between infinite-dimensional function spaces. Unlike traditional methods, NOs are resolution-agnostic, making them ideal for tasks involving data at multiple resolutions. By integrating discrete-continuous (DISCO) convolutions, a realization of the neural operator framework, we propose a unified model robust to various undersampling patterns and resolutions in compressed sensing MRI. This approach captures both local and global features of images, ensuring consistent performance and enabling advanced capabilities like zero-shot super-resolution and extended field-of-view reconstruction!
Join us as we explore how this novel framework outperforms state-of-the-art methods and sets a new benchmark in efficient, flexible MRI imaging.

We follow an unrolled network design. First, the $NO_k$ inpaints missing measurements in measurement (frequency/$k$ space). Then, the inpainted $k$-space is brought to image space through an inverse Fourier transform 𝓕$^{-1}$ and finally iteratively processed by $n$ cascades of $NO_i$ and data-consistency modules.
The $NO_k$ neural operator makes our framework agnostic to different measurement undersampling patterns, and the $NO_i$ neural operator makes the framework agnostic to different image resolutions. Accurate MRI reconstruction relies on capturing both local and global image features, and our proposed architecture incorporates inductive biases to handle both effectively. The learning in both frequency and image space allows the model to capture both local and global features of images due to the duality of the Fourier transform that connects the frequency and image space. The resolution-agnostic design also enables superresolution in both frequency and image space, allowing the extended field of view (FOV) and super-resolution of the reconstructed MR images.
The $NO_i$ is implemented as a UDNO that operates in image space and the $NO_k$ is implemented as a UDNO that operates in measurement (frequency) space. We describe our in-place resolution invariant replacement for a U-shaped architecture, the UDNO, and the DISCO convolution kernels that enable resolution invariance.
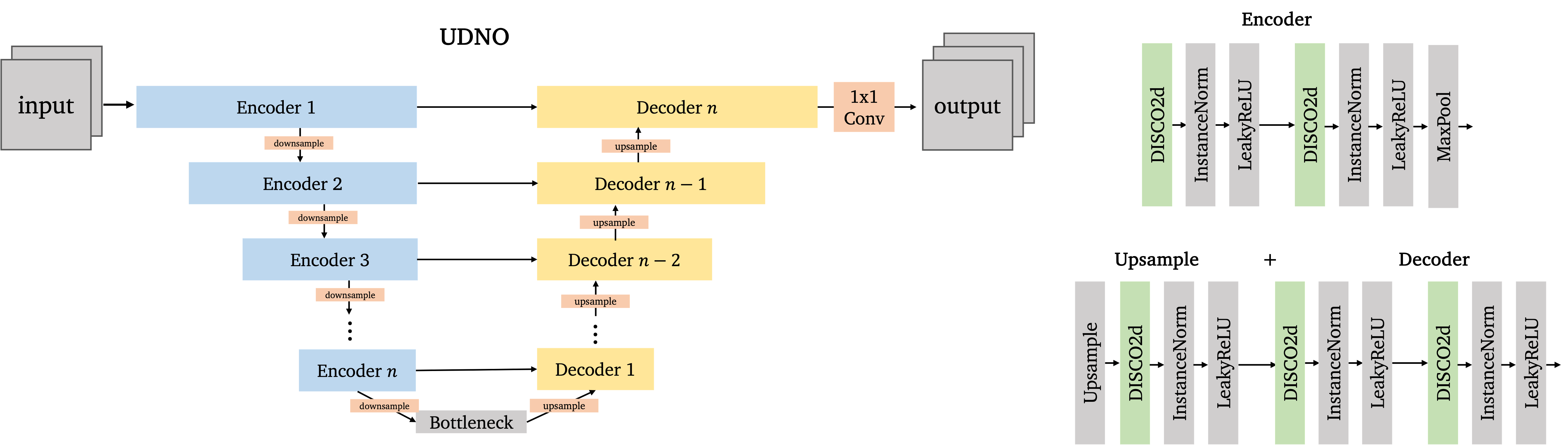
We introduce the U-Shaped DISCO Neural Operator, which is an in-place resolution invariant replacement for
the U-Net. We follow the encoder/decoder architecture of the U-Net closely, replacing conventional
convolutions with
corresponding DISCO layers. The UDNO model is available for use in the neuraloperator/nomri repository.
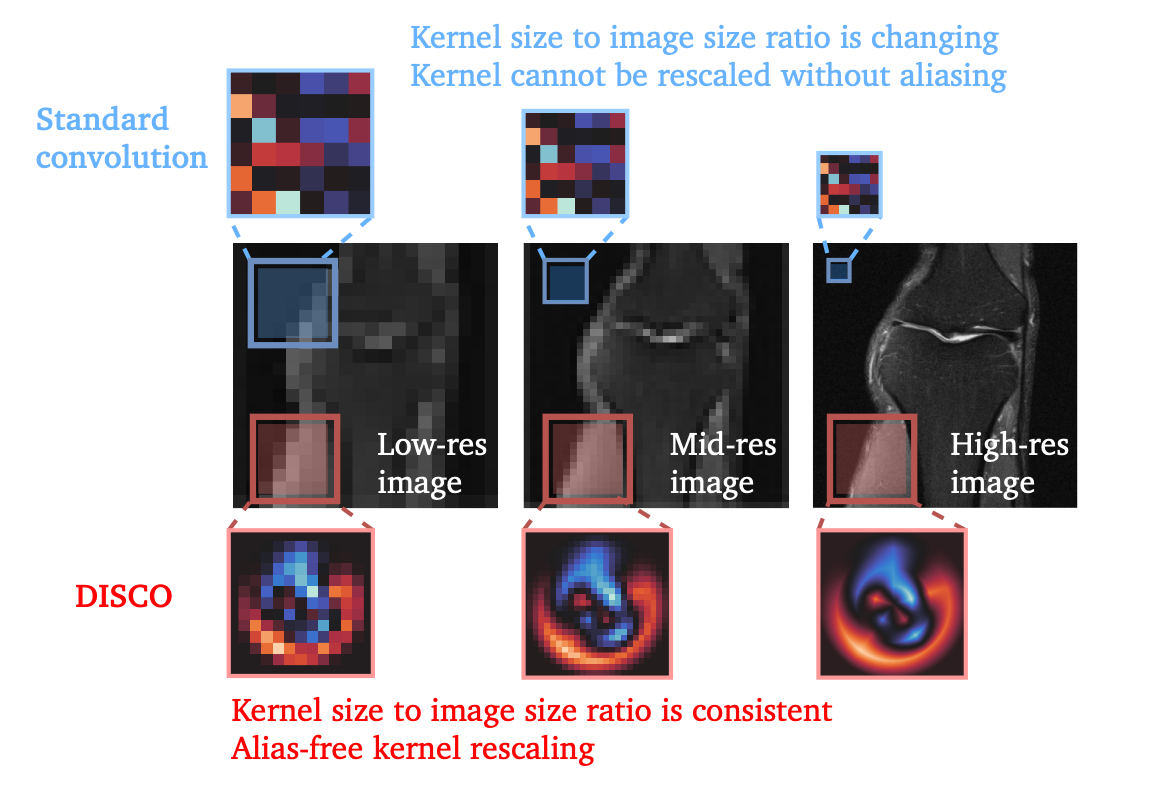
When input resolution increases, standard convolutional kernels shrink in size relative to the feature map. While kernels can be interpolated to larger sizes to mitigate some of these issues, this often introduces artifacts at new resolutions.
In contrast, DISCO kernels are parametrized in function space, ensuring that their size remains consistent across resolutions. This inherent scaling makes DISCO kernels agnostic to resolution changes.
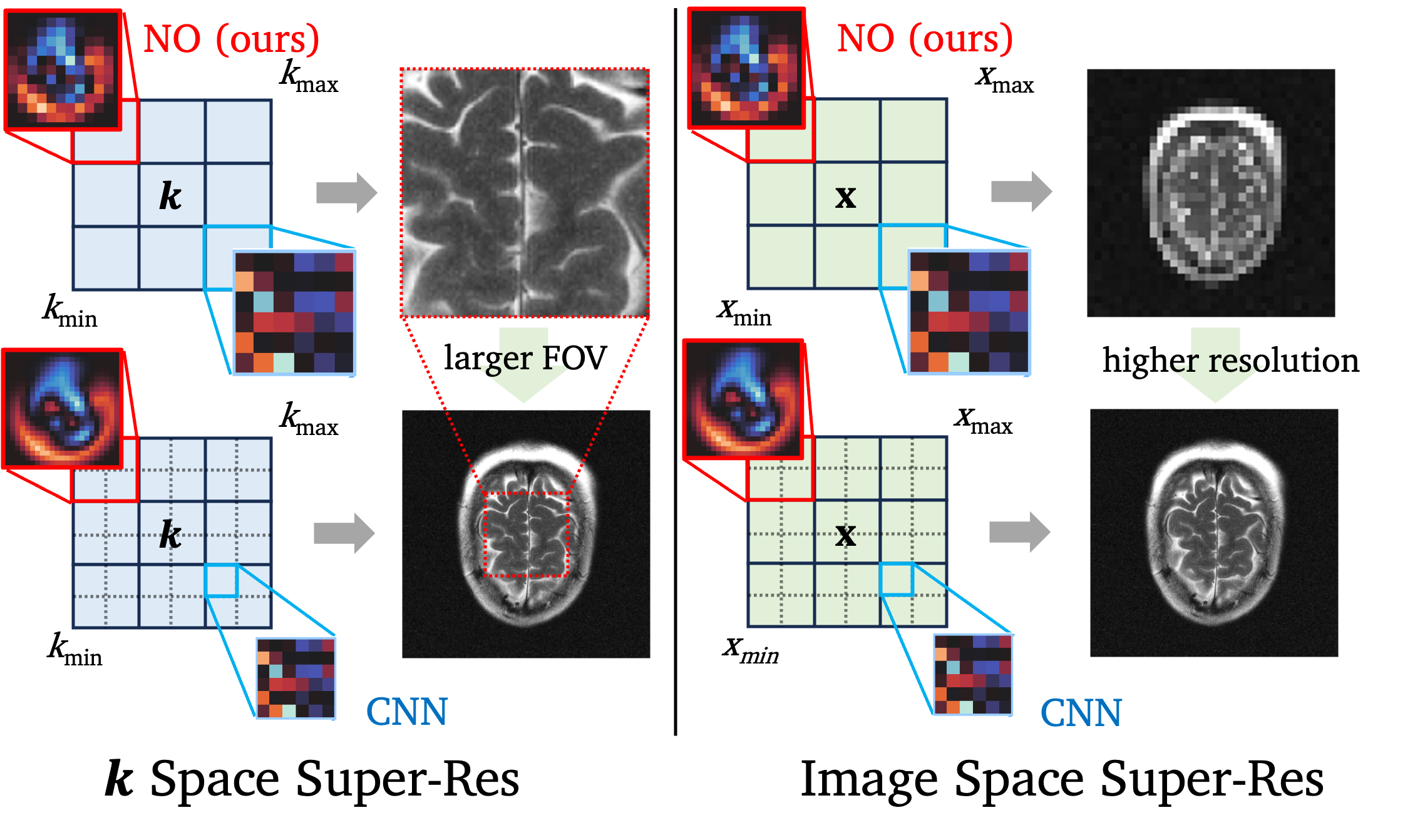
Left: Super-FOV $NO_k$. Right: Super-Resolution $NO_i$.
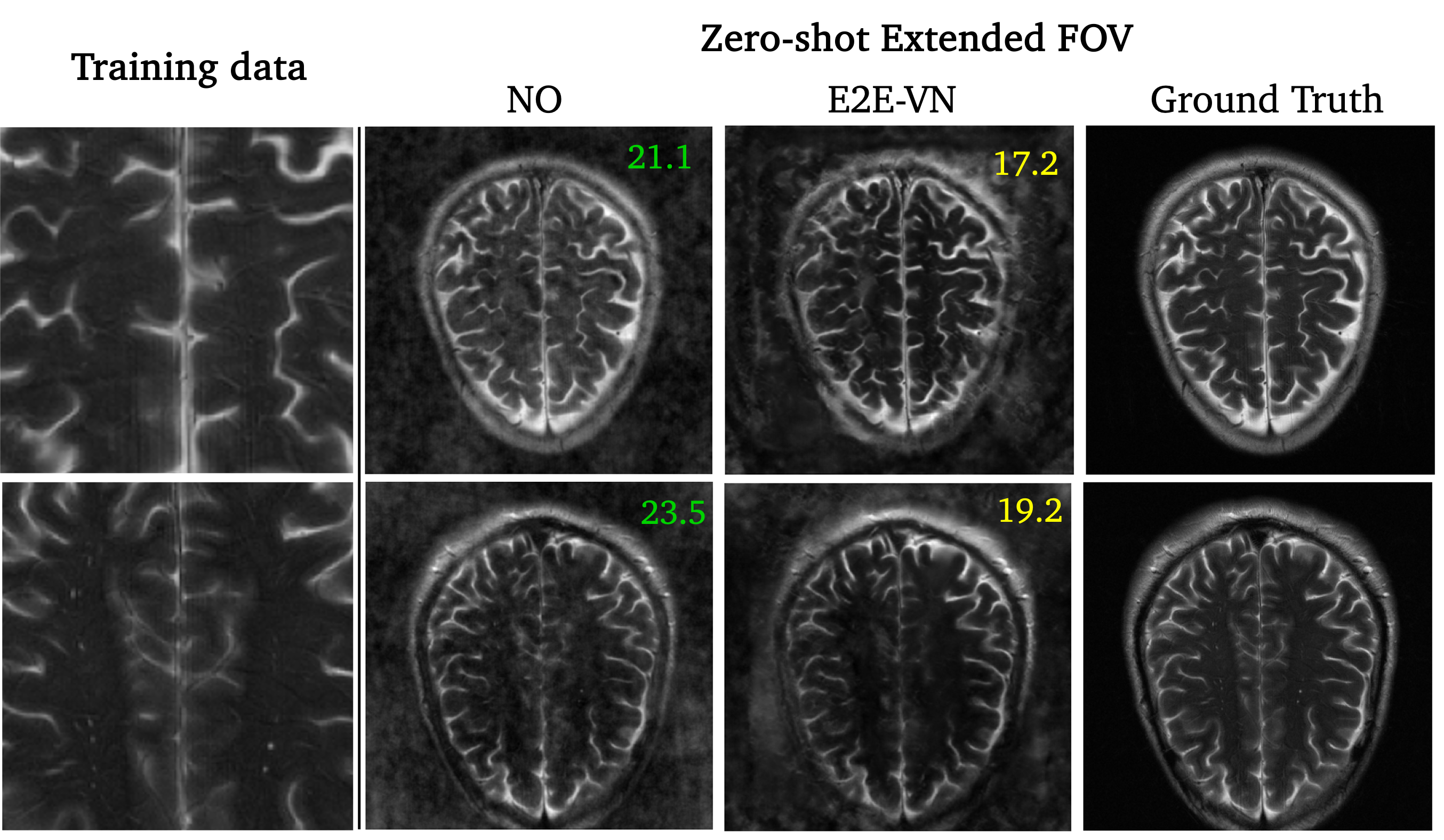
Zero-shot extended FOV reconstructions: Our NO model shows fewer artifacts and higher PSNR in the reconstructed brain slices compared to the CNN-based E2E-VN on $4\times$ Gaussian, despite neither model seeing data outside the initial $160 \times 160$ FOV during training.
Increasing resolution in $k$-space (frequency) corresponds to denser discretization between fixed minimum and maximum values, while the overall domain range remains constant. Due to the duality between frequency and image space in MRI, this corresponds to higher FOV. We demonstrate that our NO model which is trained for $160 \times 160$ low FOV reconstruction (top) can reconstruct larger FOV $320 \times 320$ images in a zero-shot setting.
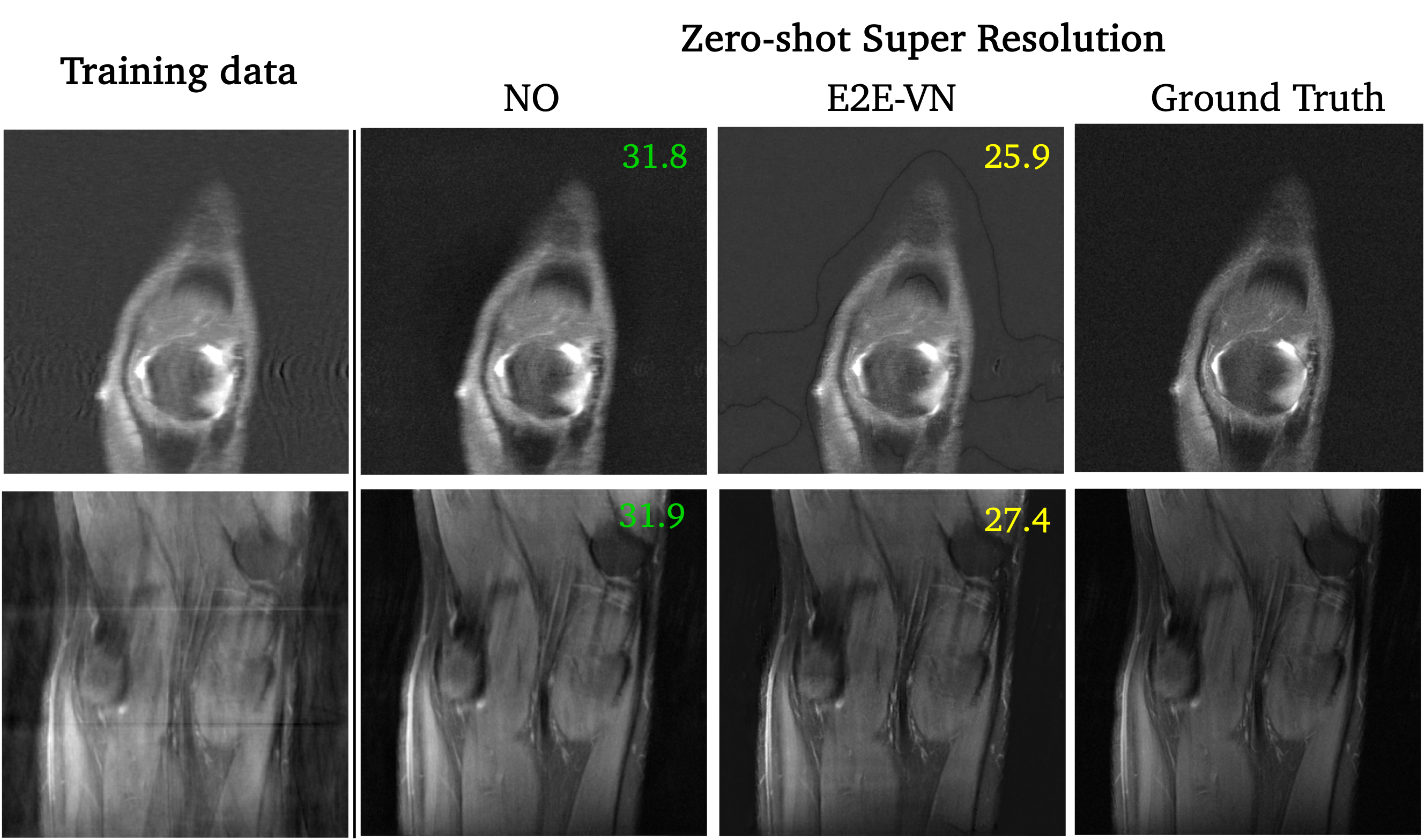
Zero-shot super-resolution reconstructions in image space on $2\times$ radial: With input resolution increased to $640 \times 640$ through bilinear interpolation, our NO model preserves reconstruction quality, while E2E-VN produces visible artifacts.
Our NO can be trained on lower resolution (image-space) $320 \times 320$ images; then our $NO_i$ can operate on higher-resolution $640 \times 640$ images for super-resolution outputs!
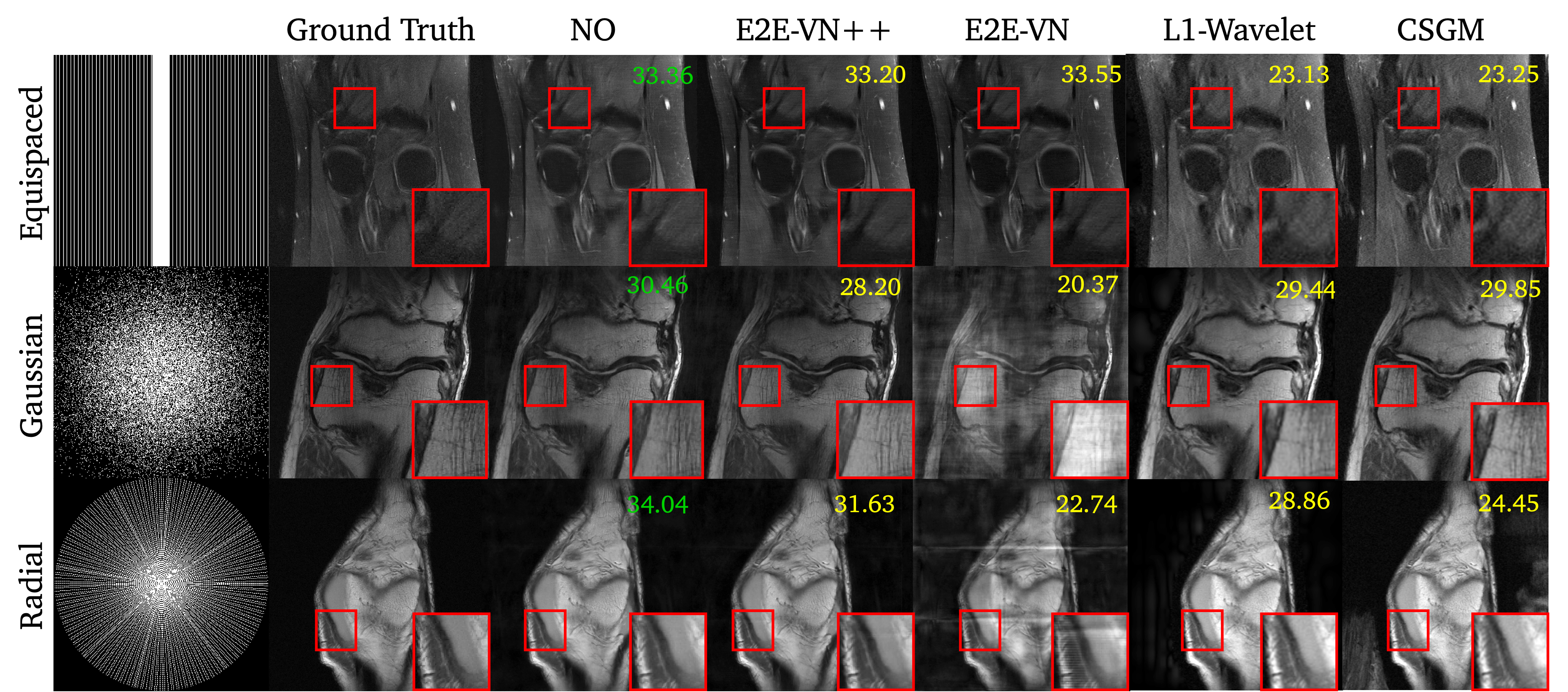
MRI reconstructions with different undersampling patterns for different methods: NO (ours), E2E-VN++, E2E-VN, L1-Wavelet (compressed sensing), and CSGM (diffusion). Our NO reconstructs high-fidelity images across various undersampling patterns.
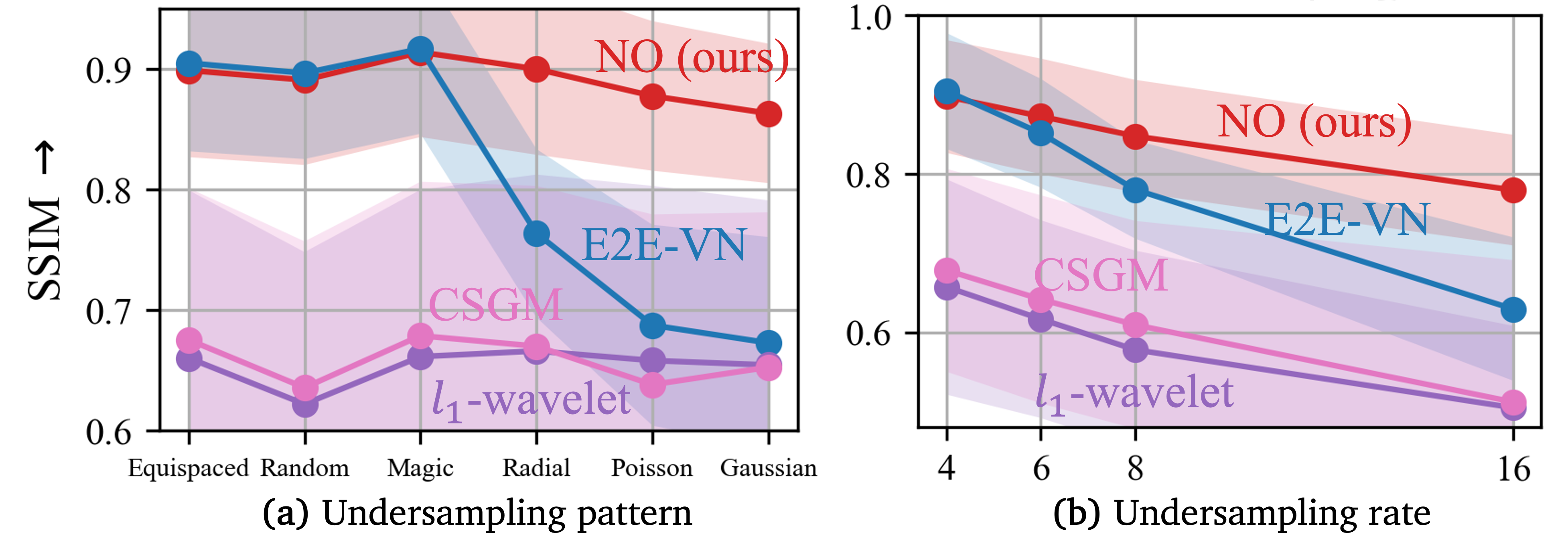
Performance across different undersampling patterns and rates of NO (ours) and baseline methods: End-to-End VarNet, diffusion and learning-free (classical). Our NO remains relatively consistent in performance when evaluated at different undersampling patterns and rates. Note that a high undersampling rate makes the task more difficult and thus a worse score is expected.
@inproceedings{jatyani2025nomri,
author = {Armeet Singh Jatyani* and Jiayun Wang* and Aditi Chandrashekar and Zihui Wu and Miguel Liu-Schiaffini and Bahareh Tolooshams and Anima Anandkumar},
title = {A Unified Model for Compressed Sensing MRI Across Undersampling Patterns},
booktitle = {Conference on Computer Vision and Pattern Recognition (CVPR) Proceedings},
abbr = {CVPR},
year = {2025}
}